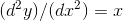Ejemplo de Integración por el método del trapecio.

El método del trapecio es un método numérico que es de gran utilidad para aproximar la integral de una función, es el método más sencillo para aproximar la integral de una función, sin embargo también es, comparativamente, el más inexacto. Ejemplificaremos la manera de aplicar el método en lápiz y papel a través de un ejemplo. 

A continuación se muestra lo formula general para la solución de una integral por el método del trapecio.

Para ejemplificar el uso de la ecuación anterior debemos plantear una ecuación para encontrar su integral. Utilizaremos la siguiente ecuación para nuestro ejemplo.

 El siguiente paso para implementar el método del trapecio es definir h. Si la integral está definida en el intervalo [a , b] entonces h se definirá de la siguiente manera. 

h=(b-a)/n

n= número de subintervalos. 

El valor de n es definido por la persona que realiza el procedimiento. 

Nota: Mientras más subintervalos se utilicen, el resultado obtenido del procedimiento será mas exacto. 

Para nuestro ejemplo utilizaremos un valor de n igual a 4, por lo tanto el valor de h quedará de la siguiente manera.

h=( 5-1)/(4)=1

Si reformulamos la ecuación del método del trapecio para utilizarlo en nuestra ecuación problema, la formula quedaría de la siguiente manera.

Nota: En cualquier ecuación que se quiera resolver por este método, tanto el primero como el ultimo termino de la ecuación serán los únicos que no estén multiplicados por 2, el resto lo estarán. 

Para efectos de lo anterior

 f(x1)= f(a)

f(x2)= f(a+h)

f(x3)=f(a+2h)

f(x4)=f(a+3h)

f(x5)=f(a+4h)

Sustituyendo términos la ecuación quedaría de la siguiente manera. 

f (a) =1

f (a+h) = f(2) = 1/2

f (a+2h) = f(3) = 1/3

f (a+3h) = f(4) = 1/4

f (a+4h) = f(5) = 1/5

Si lo revisamos, el valor real de la integral de nuestra ecuación problema es de 1.6094, por lo que al usar este método obtuvimos una muy buena estimación del valor de la integral, si hubiéramos utilizado un valor de "n" más grande hubiéramos obtenido una aproximación mucho más exacta. 

Elementos genéticos móviles.

Los Elementos genéticos móviles, también conocidos como transposones, son secuencias de ADN que tienen la capacidad de moverse de un lugar a otro a lo largo del genoma de una célula, estos elementos tienen presencia tanto en células eucariotas como en células procariotas. Los elementos genéticos móviles fueron descubiertos por primera vez hace más de cincuenta años por la genetista Bárbara McClintock, en un principió pareció que su existencia era un resultado inverosímil, sin embargo con el paso de las décadas se fue haciendo cada vez mas evidente la presencia de estos elementos en la mayoría de los organismos vivos estudiados hasta ahora.
 ¿Qué tipo de transposones existen?
Primordialmente existen dos tipos de transposones, los transposones de ADN (DNA transposons) y los retrotransposones, los cuales, a su vez, se dividen en 2 subtipos.
- Transposones de ADN. 
Los transposones de ADN reciben su nombre debido a que durante el proceso de transposición no se utilizan moléculas de ARN como intermediarios (Pray, 2008), por lo tanto, los transposones de ADN solo pueden actuar mediante el mecanismo denominado "de corte y pegado", durante este proceso entra en acción la enzima nombrada muy apropiadamente como Transposasa. Dicha enzima es codificada por el transposon, los transposones también son capaces de codificar otras proteínas, pero para los propósitos de movimiento a través del genoma la enzima Transposasa es de vital importancia, puesto que su función, una vez sintetizada, es la de "cortar" los extremos del transposon (mecanismo de corte), dejando así el nuevo fragmento de ADN libre para poder cambiar su ubicación, una vez que el fragmento llega al ADN Diana la misma enzima es responsable de integrar el transposon a la nueva ubicación (mecanismo de pegado). Los transposones de ADN se caracterizan por la presencia de una serie de repeticiones continuas de bases en los extremos del transposon, las cuales pueden tener entre 9 y 40 bases de longitud (Pray, 2008) se les conoce como repeticiones terminales invertidas (terminal inverted repeats) entre las funciones de las LTR está la de ser reconocidas por la enzima transposasa, de esa manera la enzima puede actuar exclusivamente sobre los dominios del elemento genético móvil.
Cabe destacar que la mayor diferencia que tienen este tipo de transposones con los retrotransposones es que no necesitan cambiar su información entre ADN y ARN para poder cambiar de lugar , al rededor del 2% del genoma humano está compuesto de este tipo de transposones (Pray, 2008).

Representación gráfica de las LTR y las FDR. Las FDR no son parte del transposon (Pray, 2008), debido a que después del proceso de transposición estas permanecen en su sitio original. 

-Retrotransposones. Los retrotransposones no actúan bajo el mecanismo de "corte y pegado" sino mas bien con un mecanismo de tipo replicativo. A diferencia de los transposones de ADN, los cuales cambian de un lugar a otro, los retrotransposones son capaces de replicarse y "colonizar" otras regiones del genoma mientras que el retrotransposon original continua en su ubicación inicial. Existen, a la vez, 2 tipos de retrotransposones, de acuerdo con su origen se dividen en retrotransposones retrovirales y retrotransposones no retrovirales. El proceso de transposición inicia cuando la secuencia genética propia de un retrotransposon es transcrita, las células llevan a cabo este proceso todo el tiempo a través de la enzima ARN polimeraza, este se convierte en un fragmento de mRNA (o ARN mensajero), algunas de las copias de dicho mRNA serán utilizadas para sintetizar las enzimas necesarias para lograr una transposición exitosa, esto se da gracias a que los retrotransposones tienen varios marcos de lectura ligeramente distintos, lo cual les permite contener la información necesaria para la síntesis de más de una proteína. Una vez que las enzimas necesarias han sido sintetizadas por la célula, la secuencia completa perteneciente al retrotransposon es convertida a mRNA. Es entonces que la enzima denominada como transcriptasa inversa, una especie extraña de polimeraza capaz de trasformar las cadenas de ARN en cadenas de ADN, entra en acción convirtiendo el transcrito entero de mRNA en una doble cadena de ADN. Una vez que el nuevo retrotransposon a sido convertido en ADN, es cuando se marca más la division entre retrotransposones retrovirales y no retrovirales, en el caso de los retrotransposones retrovirales entra en juego la enzima Integrasa, que es responsable de, como su nombre lo indica, integrar el elemento genético móvil en el fragmento de ADN Diana, se piensa que la nueva ubicación es elegida al azar. En el caso de los retrotransposones no retrovirales entra en juego una Endonucleasa, la cual tiene la tarea de hacer un corte en el esqueleto azúcar-fosfato del ADN Diana, con el objetivo de hacer un espacio para la inserción de la secuencia perteneciente al retrotransposon. Las funciones de ambas enzimas son muy parecidas, sin embargo tienen orígenes muy diferentes, ya que la Integrasa es una enzima de origen viral mientras que las endonucleasas son propias de los organismos vivos. En consecuencia se piensa que los retrotransposones retrovirales tienen un origen viral, es decir, son remanentes de antiguos virus que invadieron el ADN de nuestros ancestros hace ya mucho tiempo. Los retrotransposones retrovirales tienen como característica particular la presencia de repeticiones terminales invertidas (LTR), mientras que los retrotransposones no retrovirales carecen de estas secuencias, los retrotransposones retrovirales presentes en el genoma humano han perdido toda capacidad de transposición (Pray, 2008), siendo los retrotransposones o retrovirales los únicos que aun tienen dicha capacidad.

Representación gráfica del proceso de transposición de un retrotransposon.

¿Qué función tienen? Es necesario recalcar que la mayoría de los elementos genéticos móviles presentes en el cuerpo humano han perdido su capacidad de transposición debido a mutaciones que han inutilizado la acción de las enzimas que estos codifican y que son necesarias para llevar a cabo dicho proceso. Así, elementos genéticos móviles como la secuencia Alu y la secuencia LINE-1 (la secuencia LINE-1 representa al rededor del 15% del genoma humano), entre muchos otros transposones tanto de AND como retrotransposones, conforman por lo menos el 45% del genoma humano (Pace, Feschotte, 2007), pero muy pocas de estas secuencias son aún funcionales. Sin embargo, los elementos genéticos móviles si fueron de gran importancia durante el proceso evolutivo de la mayoría de los organismos complejos que conocemos, esto se concluye debido a la aparente abundancia de estas secuencias en los genomas de los organismos  más complejos, esto se debe a que el movimiento de estos elementos genéticos puede provocar mutaciones que, con el paso del tiempo, pueden resultar benéficas para los organismos portadores.

"Es una lección de humildad contemplar cómo muchas de nuestras cualidades humanas únicas podríamos debérselas a elementos genéticos parasitos" 

Los efectos que puede ejercer un elemento genético móvil dependen del lugar en el que este se inserte, si el transposon se inserta dentro de un gen podría provocar una mutación, alterando  o anulando por completo la función de dicho gen, esto se descubrió cuando un retrotransposon de tipo LINE-1 se insertó dentro del gen que codifica la información para el Factor VIII, causando hemofilia. Otras enfermedades pueden ser relacionadas con la inserción un transposon dentro de la secuencia perteneciente a un gen. Los virus son considerados elementos genéticos móviles que, además, tienen la capacidad de salir de un célula e insertarse en los genomas de otra.


Bibliografía.

- Pray, L. (2008) Transposons: The jumping genes. Nature Education 1(1):204
- Pace, J. K., & Feschotte, C. (2007). The evolutionary history of human DNA transposons: Evidence for intense activity in the primate lineage. Genome Research, 17(4), 422–432. doi:10.1101/gr.5826307

Métodos numéricos, el método de bisección.

El método de bisección en métodos numéricos es utilizado para obtener la raíz de una ecuación. El termino "raíz" se refiere al valor de x que tiene la capacidad de hacer que la ecuación planteada tenga un valor igual, o muy cercano, a cero. 

Para implementar el método de bisección en lápiz y papel primero debemos plantear una ecuación problema, nuestra ecuación problema será la siguiente.

f(x)=( x^3)+(4*x^2)-10

El siguiente paso para implementar el método es proponer un intervalo entre el cual creemos que se encuentra la raíz de la ecuación, al valor más pequeño del intervalo le llamaremos "a" y al mayor le llamaremos "b".

La única condición que debe cumplir el intervalo propuesto es que el producto de f(a) y f(b) sea menor a cero.

f(a) * f(b) < 0 

The product of f(a) and f(b) must be minor to cero for the ethod to work.

Para nuestra ecuación problema propondremos el intervalo abierto de 1 a 2.

f(a)= 1+4-10 = -5

f(b)= 8+16-10 = 14

Por lo anterior comprobamos que nuestro intervalo cumple con la condición mencionada en el punto anterior.

El siguiente paso será definir el valor de P.

P= a + (b-a)/2

Por lo tanto, para nuestro problema, P tendrá el siguiente valor.

P=1+ (2-1)/2 = 1+ (1/2)= 3/2

El siguiente paso consiste en sustituir el valor de P en nuestra ecuación.

f(P)=  (3.375)+9-10= 2.375

El siguiente paso del método será decisivo, requiere de la implementación de las siguientes 3 reglas.

- Si f (P)= 0 entonces P es la raíz de nuestra ecuación. 
If f(P) = 0 then P is the root of the equation

- Si f (P) y f(a) tiene el mismo signo, entonces la raíz de la ecuación se encontrará en el intervalo de [P , b]
If f(P) and f(a) have the same sign, then the root will be between the interval [P , b] 

- Si f(P) y f(a) tienen signo distinto, entonces la raíz de nuestra ecuación se encuentra en el intervalo de [a , P].
If f(P) and f(a) have different sign, then the root will be between the interval [a , P] 

Los anterior significa que , para nuestra ecuación problema el nuevo intervalo se encontrará en

[1 , 2.375]

f(a)= 1+4-10 = -5

f(b)= 8+16-10 = 14

f(P)=  (3.375)+9-10= 2.375

El procedimiento anteriormente señalado debe repetirse hasta que se cumpla la primera de las 3 reglas antes mencionadas, o bien, el resultado sea tan pequeño que pueda volverse cero. Por lo tanto, continuaremos con el procedimiento hasta encontrar la raíz de nuestra ecuación problema.

* Segunda iteración.

 [1 , 2.375]

f(a)= 1+4-10 = -5

f(b)= (13.39) + 22.56 - 10 = 25.95

 P= 1+ (2.375-1)/2 = 1+ 0.6875 = 1.6875

f(P)= 4.805 + 11.39 - 10 = 6.1956

*Tercera iteración [1 , 1.6875]

f(a)= 1+4-10 = -5

f(b)=  4.805 + 11.39 - 10 = 6.1956

P=1+(1.6875-1)/2 = 1+0.3437 = 1.3437

f(P) = 2.4260 + 7.222 -10 = -0.3518

*Tercera iteración [ 1.3437 , 1.6875]

f(a)= 2.4260 + 7.222 -10 = -0.3518

f(b)=  4.805 + 11.39 - 10 = 6.1956

P= 1.3437 +(1.6875-1.3437)/2= 1.5156

f(P)= 3.4813+ 9.1881 - 10 = 2.6694

*Cuarta iteración [1.3437 , 1.5156]

f(a)= 2.4260 + 7.222 -10 = -0.3518

f(b)=  3.4813+ 9.1881 - 10 = 2.6694

P= 1.3436+(1.5156 - 1.3437)/2 = 1.4296

f(P) = 2.8220 + 8.1750 - 10 = 0.9970

*Quinta iteración. [1.3437 , 1.4296]

f(a)= 2.4260 + 7.222 -10 = -0.3518

f(b) = 2.8220 + 8.1750 - 10 = 0.9970

P= 1.3437 + ( 1.4296-1.3437)/2 = 1.3866

f (P) = 2.666 + 7.69 - 10 = 0.35063

*Sexta iteración [1.3437 , 1.3866]

f(a)= 2.4260 + 7.222 -10 = -0.3518

f(b) = 2.666 + 7.69 - 10 = 0.35063

P= 1.3437+ (1.3866-1.3437)/2 = 1.36515

f(P)= 2.5441 + 7.4539 - 10 = - 0.00190

Se puede observar que en la sexta iteracion f (P) es aproximadamente cero, por lo tanto, la raíz de la ecuación es aproximadamente 1.3651.

Como se puede ver, el procedimiento es largo y tedioso, y, si te estabas preguntando para que sirve la tan mencionada raíz, pues resulta que la raíz representa un valor de x que satisface la ecuación, por lo tanto, si aplicamos este método a una ecuación cuadrática sería posible obtener el valor de x. A través del uso de este método es posible encontrar solución a ecuaciones cuadráticas  o, incluso, de niveles más altos siempre y cuando se cumplan todas las reglas antes mencionadas. Por supuesto no tendría sentido aplicar el método a mano debido a la cantidad de esfuerzo que ello representa y al desconocimiento de la cantidad de iteraciones necesarias para llegar a una solución precisa, por fortuna el uso de los lenguajes de programación hace mucho mas fácil está tarea. Si quieres saber más sobre el código en MATLAB para este procedimiento, revisa nuestra sección de Métodos numéricos en MATLAB

Ecuaciones Diferenciales

A veces al escuchar el término “ecuación diferencial” se piensa, erróneamente, que se trata de términos matemáticos demasiado especializados, hoy les explicaré lo que es una ecuación diferencial, así como el método más básico para resolver las ecuaciones diferenciales, el método de integración directa.

Para comenzar ¿Qué es una ecuación diferencial?

Una ecuación diferencial es toda ecuación que contiene derivadas. Una derivada es una función que describe el cambio en la pendiente de otra función.

Clasificación de las ecuaciones diferenciales.

Hay una serie de características a través de las cuales se puede clasificar una ecuación diferencial.

·        Por tipo. Existen 2 tipos de ecuaciones diferenciales.

-      Ecuaciones diferenciales ordinarias: La ecuación diferencial contiene derivadas de una o más variables dependientes con respecto a una sola variable independiente.

-      Ecuaciones diferenciales no ordinarias: La ecuación diferencial contiene derivadas parciales de una o más variables dependientes con respecto a dos o más variables independientes.

·        Por orden. El orden de una ecuación diferencial se refiere a la derivada de mayor orden contenida en la ecuación.

• Es una ecuación diferencial de primer orden. 

•   Es una ecuación diferencial de segundo orden, nota que la expresiónes equivalente a y'', se refiere a la segunda derivada de una ecuación que tiene solo una variable independiente. Por lo tanto, si la derivada de mayor orden en una ecuación es  y'', la ecuación será de segundo orden, si la mayor es  y''', la ecuación será de tercer orden, y así sucesivamente. 

Para implementar el método de Euler para ecuaciones diferenciales en MATLAB, visita la siguiente entrada
http://cienciaparacualquiera.blogspot.mx/2015/11/implementacion-del-metodo-de-euler-en.html

·        Por grado. El grado de una ecuación diferencial se refiere a la potencia a la que está elevada la derivada de mayor orden. El grado de una ecuación diferencial se puede describir de 2 maneras.

-      Ecuaciones diferenciales lineales:

o   La variable dependiente y todas sus derivadas son de primer grado, es decir, con exponente uno.

o   Cada coeficiente de "y" depende solamente de la variable independiente x.

-      Ecuaciones diferenciales no lineales: Son las ecuaciones que no cumplen con las características del punto anterior.

Ecuación diferencial lineal.

y y’’+ (x^2) * y= x      La ecuación no es lineal debido a que el coeficiente de una de las derivadas depende, a su vez, de la variable dependiente “y”.    

Todo lo anterior parece muy rebuscado, sin embargo carece de importancia real una vez que se ha adquirido la suficiente práctica en los métodos de solución.

Método de integración directa

El método más sencillo para resolver una ecuación diferencial es el método de integración directa, el cual solo puede ser utilizado para resolver las ecuaciones diferenciales de variables separables. Nota que el proceso de integración es el inverso que el proceso de derivación, por lo tanto el resultado de integrar una derivada es la función original.

Una ecuación diferencial de variables separables tiene la siguiente forma

La ecuación puede ser resuelta al integrar cada término de la ecuación.

∫f(x)dx+∫g(y)dy=0

Probemos la teoría resolviendo la siguiente ecuación diferencial.

-      Lo primero que se debe hacer ante una ecuación de este tipo es despejar las variables “y” y “x”, de manera que queden en lados opuestos de la igualdad.

Nota= recuerda que 1/e^x =e^(-x)

-      Una vez hecho eso, se integra cada una de las partes

                                                       

Integral por partes x=u     dv= e^(-x)     

-      Una vez hecho el proceso de integración, la ecuación queda de la siguiente manera.

La siguiente se denomina como "solución general en la forma implícita", debido a que la ecuación no está despejada a la variable y.

Solución general en la forma explícita.

Para encontrar el valor de la constante de integración es necesario plantear las condiciones iniciales del problema, para nuestro ejemplo las plantearemos de forma arbitraria.

-      Cuando x= 0    y=1, lo cual es igual a decir y(0)=1

Si se sustituyen los valores se obtiene la siguiente expresión.

Al despejar lo anterior se obtiene que

El valor del número de Euler es aproximadamente 2.71, por lo tanto.

Así, la solución para la ecuación diferencial queda de la siguiente manera

Sustituyendo con el recién encontrado valor de y, nuestra ecuación inicial quedará de la siguiente manera.

Dicha ecuación ahora estará disponible para cualquier uso que dispongamos.