Métodos Científicos : Ecuaciones Diferenciales

A veces al escuchar el término “ecuación diferencial” se piensa, erróneamente, que se trata de términos matemáticos demasiado especializados, hoy les explicaré lo que es una ecuación diferencial, así como el método más básico para resolver las ecuaciones diferenciales, el método de integración directa.

Para comenzar ¿Qué es una ecuación diferencial?

Una ecuación diferencial es toda ecuación que contiene derivadas. Una derivada es una función que describe el cambio en la pendiente de otra función.

Clasificación de las ecuaciones diferenciales.

Hay una serie de características a través de las cuales se puede clasificar una ecuación diferencial.

· Por tipo. Existen 2 tipos de ecuaciones diferenciales.

- Ecuaciones diferenciales ordinarias: La ecuación diferencial contiene derivadas de una o más variables dependientes con respecto a una sola variable independiente.

- Ecuaciones diferenciales no ordinarias: La ecuación diferencial contiene derivadas parciales de una o más variables dependientes con respecto a dos o más variables independientes.

· Por orden. El orden de una ecuación diferencial se refiere a la derivada de mayor orden contenida en la ecuación.

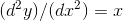Es una ecuación diferencial de primer orden.

Es una ecuación diferencial de segundo orden, nota que la expresiónes equivalente a y'', se refiere a la segunda derivada de una ecuación que tiene solo una variable independiente. Por lo tanto, si la derivada de mayor orden en una ecuación es y'', la ecuación será de segundo orden, si la mayor es y''', la ecuación será de tercer orden, y así sucesivamente.

Para implementar el método de Euler para ecuaciones diferenciales en MATLAB, visita la siguiente entrada
http://cienciaparacualquiera.blogspot.mx/2015/11/implementacion-del-metodo-de-euler-en.html

· Por grado. El grado de una ecuación diferencial se refiere a la potencia a la que está elevada la derivada de mayor orden. El grado de una ecuación diferencial se puede describir de 2 maneras.

- Ecuaciones diferenciales lineales:

o La variable dependiente y todas sus derivadas son de primer grado, es decir, con exponente uno.

o Cada coeficiente de "y" depende solamente de la variable independiente x.

- Ecuaciones diferenciales no lineales: Son las ecuaciones que no cumplen con las características del punto anterior.

Ecuación diferencial lineal.

y y’’+ (x^2) * y= x La ecuación no es lineal debido a que el coeficiente de una de las derivadas depende, a su vez, de la variable dependiente “y”.

Todo lo anterior parece muy rebuscado, sin embargo carece de importancia real una vez que se ha adquirido la suficiente práctica en los métodos de solución.

Método de integración directa

El método más sencillo para resolver una ecuación diferencial es el método de integración directa, el cual solo puede ser utilizado para resolver las ecuaciones diferenciales de variables separables. Nota que el proceso de integración es el inverso que el proceso de derivación, por lo tanto el resultado de integrar una derivada es la función original.

Una ecuación diferencial de variables separables tiene la siguiente forma

La ecuación puede ser resuelta al integrar cada término de la ecuación.

∫f(x)dx+∫g(y)dy=0

Probemos la teoría resolviendo la siguiente ecuación diferencial.

- Lo primero que se debe hacer ante una ecuación de este tipo es despejar las variables “y” y “x”, de manera que queden en lados opuestos de la igualdad.

Nota= recuerda que 1/e^x =e^(-x)

- Una vez hecho eso, se integra cada una de las partes

Integral por partes x=u dv= e^(-x)

- Una vez hecho el proceso de integración, la ecuación queda de la siguiente manera.

La siguiente se denomina como "solución general en la forma implícita", debido a que la ecuación no está despejada a la variable y.

Solución general en la forma explícita.

Para encontrar el valor de la constante de integración es necesario plantear las condiciones iniciales del problema, para nuestro ejemplo las plantearemos de forma arbitraria.

- Cuando x= 0 y=1, lo cual es igual a decir y(0)=1

Si se sustituyen los valores se obtiene la siguiente expresión.